Random subspaces of a tensor product (I)

This is the first post in a series about a problem inside RMT $\cap$ QIT that I have been working on for some time now [cn2,bcn]. Since I find it to be very simple and interesting, I will present it in a series of blog notes that should be accessible to a large audience. I will also use this material to prepare the talks I will be giving this summer on this topic ;).

In what follows, all vector spaces shall be assumed to be complex and $k \leq n$ are fixed constants. For a vector $y \in \mathbb R^k$, the symbol $y^\downarrow$ denotes its ordered version, i.e. $y$ and $y^\downarrow$ are the same up to permutation of coordinates and $y^\downarrow_1 \geq \cdots \geq y^\downarrow_k$.

1. Singular values of vectors in a tensor product

Using the non-canonical isomorphism $\mathbb C^k \otimes \mathbb C^n \simeq \mathbb C^k \otimes (\mathbb C^n)^*$, one can see any vector
$!\mathbb C^k \otimes \mathbb C^n \ni x = \sum_{i=1}^k \sum_{j=1}^n x_{ij} e_i\otimes f_j$
as a matrix
$!\mathcal M_{k \times n} \ni X = \sum_{i=1}^k \sum_{j=1}^n x_{ij} e_if_j^*.$
In this way, by using the singular value decomposition of the matrix $X$ (keep in mind that we assume $k \leq n$), one can write
$!x = \sum_{i=1}^k \sqrt{\lambda_i} e’_i \otimes f’_i,$
where $(f’_i)$, resp. $(g’_i)$ are orthonormal families in $\mathbb C^k$, resp. $\mathbb C^n$. The vector $\lambda = \lambda(x) \in \mathbb R_+^{k}$ is the singular value vector of $x$ and we shall always assume that it is ordered $\lambda(x) = \lambda(x)^\downarrow$. It satisfies the normalization condition
$!\sum_{i=1}^k \lambda_i(x)= |x|^2.$
In particular, if $x$ is a unit vector, then $\lambda(x) \in \Delta^\downarrow_k$, where $\Delta_k$ is the probability simplex
$! \Delta_k = \left\{ y \in \mathbb R_+^k \, : \, \sum_{i=1}^k y_i = 1\right\}$
and $\Delta^\downarrow_k$ is its ordered version.

In QIT, the decomposition of $x$ above is called the Schmidt decomposition and the numbers $\lambda_i(x)$ are called the Schmidt coefficients of the pure state $

x \rangle$.

2. The singular value set of a vector subspace

Consider now a subspace $V \subset \mathbb C^k \otimes \mathbb C^n$ of dimension $\dim V = d$ and define the set
$! K_V = \{\lambda(x) \, : \, x \in V \text{ and } |x| = 1 \} \subseteq \Delta^\downarrow_k,$
called the singular value subset of the subspace $V$.

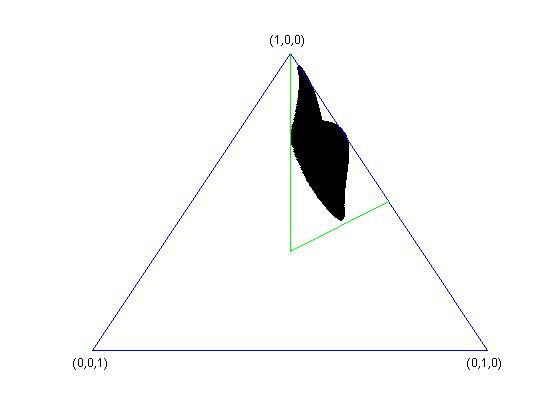
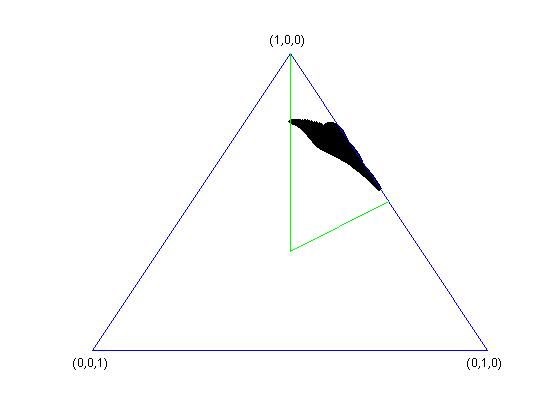
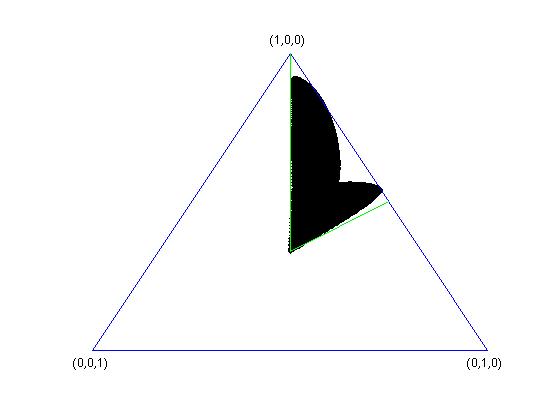
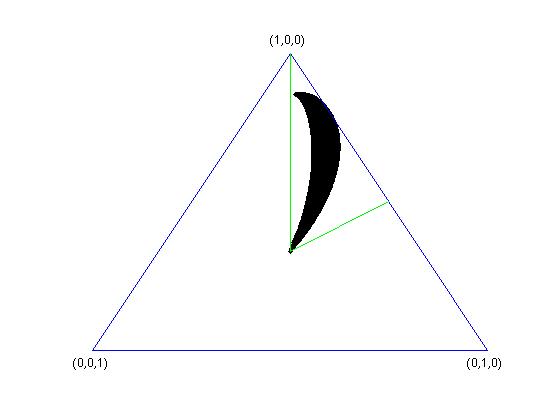
Below are some examples of sets $K_{V}$, in the case $k=3$, where the simplex $\Delta_{3}$ is two-dimensional. In all the four cases, $k=n=3$ and $d=2$. In the last two pictures, one of the vectors spanning the subspace $V$ has singular values $(1/3,1/3,1/3)$.

3. Basic properties

Below is a list of very simple properties of the sets $K_{V}$.

Proposition 1. The set $K_V$ is a compact subset of the ordered probability simplex $\Delta_k^\downarrow$ having the following properties:

1. Local invariance: $K_{(U_1 \otimes U_2)V} = K_V$, for unitary matrices $U_1 \in \mathcal U(k)$ and $U_2 \in \mathcal U(n)$.
2. Monotonicity: if $V_1 \subset V_2$, then $K_{V_1} \subset K_{V_2}$.
3. If $d=1$, $V=\mathbb C x$, then $K_V={\lambda(x)}$.
4. If $d > (k-1)(n-1)$, then $(1,0,\ldots,0) \in K_V$.

Proof: The first three statements are trivial. The last one is contained in [cmw], Proposition 6 and follows from a standard result in algebraic geometry about the dimension of the intersection of projective varieties.

4. So, what is the problem ?

The question one would like to answer is the following:

How does a typical $K_V$ look like ?

In order to address this, I will introduce random subspaces in the next post future. In the next post, I look at the special case of anti-symmetric tensors.

References

[bcn] S. Belinschi, B. Collins and I. Nechita, Laws of large numbers for eigenvectors and eigenvalues associated to random subspaces in a tensor product, to appear in Invent. Math.

[cn2] B. Collins and I. Nechita, Random quantum channels II: Entanglement of random subspaces, Rényi entropy estimates and additivity problems, Adv. in Math. 226 (2011), 1181–1201.

[cmw] T. Cubitt, A. Montanaro and A. Winter, On the dimension of subspaces with bounded Schmidt rank, J. Math. Phys. 49, 022107 (2008).