Counting meanders

We have, with Moto Fukuda, a new paper on the arXiv, Enumerating meandric systems with large number of components, which deals with the enumeration of meandric systems.

In combinatorics, a meander on $2n$ points is a closed, self-avoiding plane curve, which intersects a given line $2n$ times. Below, the meanders of a river (Rio Cauto, in Cuba) and a mathematical meander are represented.

The following more general objects are considered in the literature.

Definition 1. A meandric system on $2n$ points with $r$ connected components is a collection of $r$ non-intersecting closed curves, which cross a given line $2n$ times. A meander is a meandric system with $1$ component.

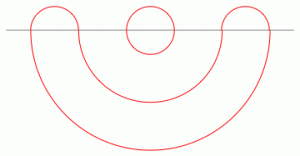
Below are represented two meandric systems on $6$ points, with $2$, respectively $3$ connected components.

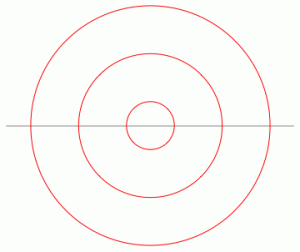
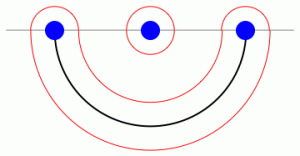
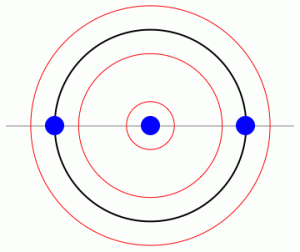
One easily recognizes the diagrams above and below the horizontal line: these are non-crossing pairings, a subclass of non-crossing partitions. Non-crossing pairings on $2n$ points are known to be in bijection with (general) non-crossing partitions on $n$ points, through an operation called fattening; in the picture below, the same meanders as above are depicted, together with the corresponding non-crossing partitions on $n=3$ points; see how the meander (red) is a “fattening” of the pair of non-crossing partitions (black).

In our paper, we study meandric systems on $2n$ points with $n-r$ connected components, for some fixed parameter $r$. We obtain the general form of the generating function for the number $M_n^{(n-r)}$ of such meanders, with exact expressions for $r \leq 6$. Some trivial observations can be made right from the start. First, we have seen that meandric systems are in bijection with pairs of non-crossing partitions. Since non-crossing partitions are counted by Catalan numbers, we have

\[\displaystyle \sum_{c=1}^n M_n^{(c)} = \mathrm{Cat}_n^2.\]

Note also that meandric systems with a maximal number of connected components (see the example on the right in the previous two pictures) correspond to the case where the two non-crossing partitions $\alpha, \beta$ defining the meander are equal $\alpha = \beta$, and thus

$\displaystyle M_n^{(n)} = \mathrm{Cat}_n.$

To compute the numbers $M_n^{(n-1)}$, it is not hard to see that the two non-crossing partitions $\alpha$ and $\beta$ must be somehow “close”. To make this precise, we consider another key bijection, the one between non-crossing partitions and the so-called geodesic permutations. In his seminal work Some properties of crossings and partitions, Biane realized that non-crossing partitions are in bijection with the following set of permutations

$ \displaystyle \mathcal S_n^{NC} := \{\alpha \in \mathcal S_n \, : \, \|\alpha\| + \|\alpha^{-1} \pi \| = \|\pi \| = n-1\},$

where $\pi$ is the full-cycle permutation $\pi = (1 2 \cdots n)$ and $\| \cdot \|$ is the length function of permutations: $\|\alpha\|$ is the minimal number of transpositions which multiply to $\alpha$. All these ideas are discussed in Lecture 23 of the excellent monograph of Nica and Speicher. In this framework, it has been known for some time that meanders on $2n$ points with $c$ connected components are in bijection with the set

$ \displaystyle \{ \alpha, \beta \in \mathcal S_n^{NC} \, : \, \|\alpha^{-1}\beta\| = n-c\}.$

In particular, for $c = n-1$, only pairs of geodesic permutations which differ by only one transposition contribute; one can easily show then

$ \displaystyle M_n^{(n-1)} = 2 \binom{2n}{n-2}.$

In our paper, we use the moment-cumulant formula from Free Probability Theory to show that, for fixed $r$, the generating function for the number of meanders on $2n$ points with $n-r$ connected components

$ \displaystyle F_r(t) = \sum_{n=r+1}^\infty M_n^{(n-r)}t^n,$

after the change of variables $t=w/ (1+w)^2$, reads

$! \displaystyle F_r(t) = \sum_{n=r+1}^\infty M_n^{(n-r)} \frac{w^n}{(1+w)^{2n}} = \frac{w^{r+1}(1+w)}{(1-w)^{2r-1}} P_r(w),$

where $P_r(w)$ are polynomials of degree at most $3(r-1)$. With the help of a computer, we find these polynomials up to $r=6$. We show that such meandric systems are made of simple building blocks, called irreducible meanders. Irreducible meanders were introduced by Lando and Zvonkin here, and they were recently featured in Andu Nica‘s recent paper.

Let me close this post by mentioning what is probably the most important problem related to the enumeration of meanders (on which we do not touch upon): the asymptotic growth of meanders. This problem and the one we discuss in our paper sit at opposite ends of the spectrum with respect to the number of components.

The sequence of meandric numbers $(M_n^{(1)})_n$ is conjectured to grow like

$ \displaystyle M_n^{(1)} \sim C \rho^n n^{-\kappa},$

for some constants $C, \rho, \kappa$. The exponential rate has been shown to satisfy $11.380 \leq \rho \leq 12.901$. The polynomial speed is conjectured to be exactly $\kappa = (29+\sqrt{145})/12$.

The meandric numbers $M_n^{(1)}$ have a very simple geometric interpretation: they count diameters in the metric space $(\mathcal S_n^{NC}, \| \cdot \|)$:

\[\displaystyle M\_n^{(1)} = \\{ \\alpha, \\beta \\in \\mathcal S\_n^{NC} \\, : \\, \\|\\alpha^{-1}\\beta\\| = n-1\\} |.\]

The asymptotic behavior of the sequence $M_n^{(1)}$ is largely open. Old and recent results suggest that solving this many-faceted problem might require some new insight or techniques.