Bipartite unitary operators and quantum Latin squares
Tristan Benoist and I have just arXived our paper On bipartite unitary matrices generating subalgebra–preserving quantum operations. We characterize the set of bipartite unitary operators which give quantum operations preserving some subalgebra of the state space, independently of the state of the coupled environment. The main results in the paper deal with the cases of (block-)diagonal algebras and tensor algebras. I obtained similar results for different classes of quantum channels in a previous paper.
In this post I would like to discuss a marginal problem discussed in the preprint, that of quantum Latin squares. Latin squares are combinatorial objects which have received a lot of attention: they are simple but deep mathematical objects, and have found many applications, mainly in statistics, experience design, and information theory.
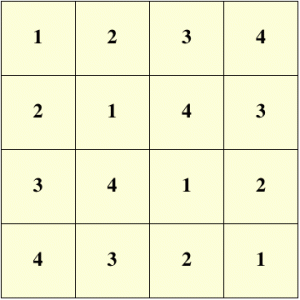
**Definition 1** *A $n \\times n$ Latin square is a matrix $L \\in M\_n(\\{1,2, \\ldots, n\\})$ with the property that each row and each column of $L$ are permutations of $\\{1,2,\\ldots, n\\}$.*
Here is an example of a Latin square of size $4$:
We are interested in a ”vector space” version of Latin squares, called quantum Latin squares, a notion introduced in the recent work of Musto and Vicary. The generalization is obtained via the classical information $\leftrightarrow$ quantum information dictionary, where alphabets are replaced by vector spaces and letters by unit vectors in those spaces.
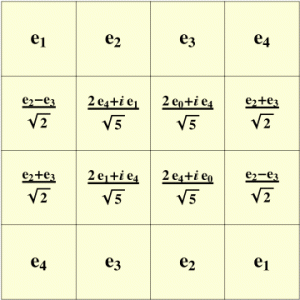
**Definition 2** *A $n \\times n$ quantum Latin square (QLS) is a $3$-tensor $X \\in M\_n(\\mathbb C^n)$ with the property that the vectors in each row and each column of $X$ form orthonormal bases of $\\mathbb C^n$.*
Below is an example of a $4 \times 4$ QLS, taken from Musto and Vicary’s paper, where $\{e_1,e_2,e_3,e_4\}$ is a basis of $\mathbb C^4$.
One can make some trivial observations right off the bat. First, the elements of a QLS $X$ must have unit Euclidean norm $\|x_{ij}\| =1$. The condition in the definition can be stated using the following matrices, having the vectors of $X$ as columns $!\begin{align*} R_i &= \sum_{j=1}^n x_{ij}e_j^*\\ C_j &= \sum_{i=1}^n x_{ij}e_i^*, \end{align*}$ for some fixed orthonormal basis $\{e_1, \ldots, e_n\}$ of $\mathbb C^n$. Then, $X$ is a QLS iff the $2n$ matrices $R_1, \ldots R_n$, $C_1, \ldots, C_n$ are unitary operators. Moreover, using these matrices, we can define a natural ”distance” function to the set $\mathcal{QLS}_n$ of $n \times n$ quantum Latin squares
$! \displaystyle d(X)^2 = \sum_{i=1}^n \|R_iR_i^* – I_n\|_2^2 + \sum_{j=1}^n \|C_jC_j^* – I_n\|_2^2.$
Every classical latin square $L$ can be seen as a quantum Latin square by using the same basis for all rows and columns: $x_{ij} = e_{L_{ij}}$. For $n \geq 4$, there exist moreover purely ”quantum” examples, such as the one pictured above. The set of $n \times n$ quantum Latin squares $\mathcal{QLS}_n$ is a real algebraic variety, since the unitarity conditions for the matrices $R_i$ and $C_j$ can be expressed as polynomial equations in the $2n^3$ variables $\operatorname{Re}(x_{ij})$, $\operatorname{Im}(x_{ij})$.
In our paper, QLS appear in connection to bipartite unitary operators $U \in \mathcal U(n^2)$ with the property that for all ancilla space density matrices $\beta \in M_{n}^{1,+}(\mathbb C)$, the quantum channel
$! \displaystyle T_{\beta}(\rho) = [\operatorname{id} \otimes \operatorname{Tr}](U (\rho \otimes \beta)U^*)$
leaves the diagonal subalgebra $D_n \subseteq M_n(\mathbb C)$ invariant (see Theorem 4.4).
We raise the question of finding a natural probability measure of the set $\mathcal{QLS}_n$. We propose such a measure, based on a non-commutative analog of the Sinkhorn-Knopp algorithm (see here and here for the original papers). The following algorithm is discussed in our paper. Below, we make use of an operator $\operatorname{Pol}$, which returns the angular part of the polar decomposition: if $X = UP$ is the polar decomposition of $X$, then $\operatorname{Pol}(X) = U$; in case the polar decomposition is not unique, one of the valid decompositions is considered.
- Input: The dimension $n$ and an error parameter $\varepsilon >0$
- Start with $x_{ij}$ independent uniform points on the unit sphere of $\mathbb C^n$.
- While $X$ is $\varepsilon$-far from $\mathcal{QLS}n$, do the steps (4-6)
- $\qquad$ Define the matrix $Y$ by making the rows of $X$ unitary: $! \displaystyle \forall i \in [n], \qquad y_{ij} = \operatorname{Pol}\left( \sum_{s=1}^n x_{is}e_s^* \right) \cdot e_j.$
- $\qquad$ Define the matrix $Z$ by making the rows of $Y$ unitary: $! \displaystyle \forall j \in [n], \qquad z_{ij} = \operatorname{Pol}\left( \sum_{s=1}^n y_{sj}e_s^* \right) \cdot e_i.$
- $\qquad$ $X \leftarrow Z$.
- Output: $X$, an $\varepsilon$-approximate QLS.
We conjecture that the algorithm above converges for almost any choice of the $n^2$ random points at step (2). We have some numerical evidence for this claim, as well as a convergence proof for a close variant of the problem, where we replace the vector entries of the matrix $X$ by positive definite matrices (see the appendix of our paper).
The algorithm above was also discussed in a paper with Teo Banica on the quantum permutation group $S_N^+$; there, we were interested in the probability measure induced on $\mathcal{QLS}_n$ by the uniform measure in step (2).
Finally, let me mention that there exists a different non-commutative generalization of the Sinkhorn algorithm, introduced by Gurvits in his paper where he shows that the weak membership problem for the set of separable states is NP-hard.